This tutorial builds on the conceptual ET-Tutorial and the physical soil column model

Getting \(ET_{act}\) from \(ET_{pot}\) for each layer

In order to calculate the water loss to the atmosphere from \(ET_{pot} [\frac{mm}{day}]\), cmf needs a connection from each soil layer to the atmospheric boundary condition. Each cell has a transpiration and an evaporation boundary object, which can be used for this task.

\[ q_{T_{pot}}\left[\frac{m^3}{day}\right]=f_r \cdot ET_{pot}\left[\frac{mm}{day}\right]A_{cell}[m^2]\frac{1 m}{1000 mm} \]

where:

\(f_r=\frac{R_{layer}}{\sum_{i=0}^{layers}{R_i}}\) the root mass in this layer per total root mass at this cell.
\(A_{cell}\) is the area of the cell

To limit water uptake from the soil layer according to its water content, cmf uses a Feddes like approach: The flux is 0, when the matrix potential \(\Psi_M\) is below wilting point. If the matrix potential is below -5m, the limitation is linearly scaled towards the wilting point and above -5m there is no water limitation:

\[ q_{T_{act}}= q_{T_{pot}}\begin{cases} 1 & \Psi_M>-5m \\ 1+\frac{\Psi_M + 5}{155} & \Psi_M>-160m \\ 0 & \Psi_M<-160 m\end{cases} \]

Setting the root content \(f_r\)

In principle, there are two ways to define the root content, set the root content fraction for each layer or define the root depth for the cell

a) set the root content directly

Soil layers have the property rootfraction that can be set. It is your responsibility to ensure that the sum of all rootfractions is 1.

for l in cell.layers[:5]:

l.rootfraction = 0.2

If you have never set the rootfraction method b) is used.

b) set the root depth for the cell

If the rootfraction of a layer has never been set, the root fraction of the layers are calculated from the RootDepth and fraction_at_rootdepth properties of the cell's vegetation object. RootDepth is the depth of the rooting zone of the cell in m. If fraction_at_rootdepth is 1, a uniform distribution of roots until RootDepth is used. If fraction_at_rootdepth is between 0..1, then an exponential decline of the root content is used. 1-fraction_at_rootdepth of the root mass is then below RootDepth.

In this example we will get the same result as in a):

cell.vegetation.RootDepth = 0.5

Here we will have 80% of the root content in the upper 40cm, and the other 20% below using an exponential decline of the root content:

cell.vegetation.RootDepth = 0.4

cell.vegetation.fraction_at_rootdepth = 0.8

If you do nothing, the RootDepth default value of 0.25 is used.

Results

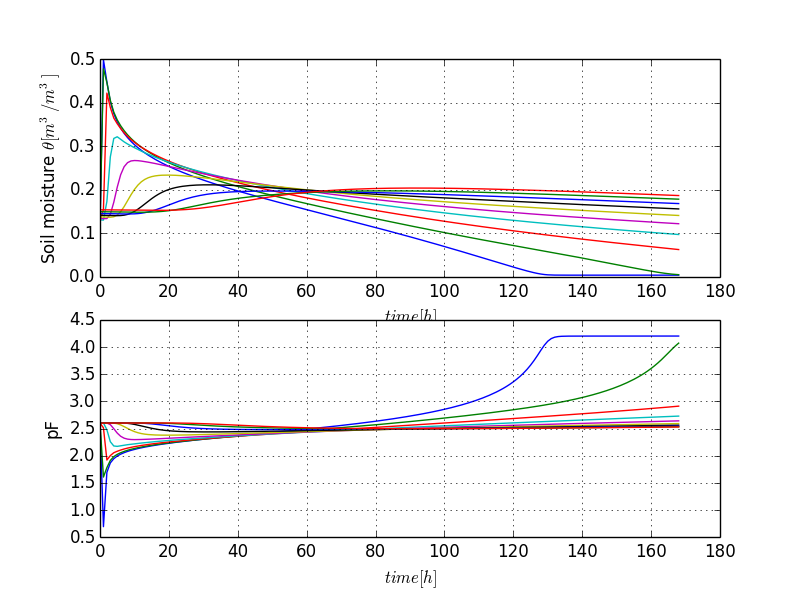
The physical soil column model results in the figure, using transpiration with a uniform root distribution and super high constant potential transpiration rate of 20 mm/day.